Comparaison de fractions - Séquence complète : 1ere Secondaire

Séquence complète sur la comparaison de fractions pour le : 1ere Secondaire

Notions sur les “opérations sur les fractions”

Cours sur la comparaison de fractions pour le : 1ere Secondaire

Pour comparer deux fractions c’est-à-dire, dire quelle est la plus grande et quelle est la plus petite, il y a 5 méthodes :

1 ère méthode : Si les fractions ont le même dénominateur.

Si deux fractions ont le même dénominateur, la plus petite est celle qui a le plus petit numérateur.

Exemple :
5/13<9/13

: 1ere Secondaire méthode : Si les fractions ont le même numérateur.

Si deux fractions ont le même numérateur, la plus petite est celle qui a le plus grand dénominateur.

Exemple :
5/19<5/13

: 1ere Secondaire méthode : On les réduit au même dénominateur.

Exemple :
5/7<16/21

Ces deux fractions n’ont pas le même dénominateur.
Ces deux fractions n’ont pas le même numérateur.

On les réduit au même dénominateur
5/7=(5×3)/(7×3)=15/21

15/21<16/21

: 1ere Secondaire méthode : On compare chacune d’elles avec l’unité.

Toutes les fractions dont le numérateur est égal au dénominateur sont égales à 1.
Toutes les fractions dont le numérateur est inférieur au dénominateur sont inférieures à 1.
Toutes les fractions dont le numérateur est supérieur au dénominateur sont supérieures à 1.

Exemple :
5/7<8/3

En effet :
5/7 <1 et 8/3 >1

: 1ere Secondaire méthode : On calcule les quotients.

On compare les valeurs exactes ou approchées des deux quotients :

421/79<87/16
En effet :
421/79≈ 5,33

87/16≈ 5,44

Propriété

Toute fraction peut être encadrée par deux entiers consécutifs.
Si q est le quotient de la division euclidienne de a par b
q<a/b< q+1
Par exemple : 121=7 ×17+2

Donc :
17<121/7<18

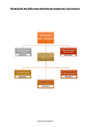
Récapitulatif des différentes méthodes de comparaison des fractions

Exercices avec correction sur la comparaison de fractions pour le : 1ere Secondaire

Consignes pour ces exercices :

Comparer les fractions suivantes :

Observer la droite graduée ci-dessous :

Entourer :

Ecrire les fractions suivantes sous forme de fractions ayant 24 pour dénominateur, puis les ranger dans l’ordre croissant :

Encadrer, par deux entiers consécutifs, les fractions suivantes :

1 – Comparer les fractions suivantes :

13/4 et 13/7
1/12 et 1/7

8/17 et 8/3
82/325 et 97/325

18/17 et 7/17
31/4 et 49/4

2 – Comparer les fractions suivantes

6/7 et 37/42
3/4 et 5/8

191/840 et 19/84
11/12 et 5/6

3 – Observer la droite graduée ci-dessous :

Après avoir placé les nombres suivants sur cette droite graduée, les ranger dans l’ordre croissant :
1/3 ; 13/12 ; (7 )/6 ; 3/4 ; 19/12

Evaluation, bilan, contrôle avec la correction sur la comparaison de fractions pour la 1ere Secondaire .

Compétences évaluées
Comparer des fractions en utilisant différentes méthodes
Ranger des fractions en utilisant différentes méthodes
Encadrer des fractions par deux entiers consécutifs

Consignes pour cette évaluation, bilan et contrôle :

Exercice N°1

Compléter les phrases suivantes :
Si deux fractions ont le même numérateur, la plus petite est :
celle qui a ……………………………………………………………………………
Si deux fractions ont le même dénominateur, la plus petite est :
celle qui a ……………………………………………………………………………

Exercice N°2

Ranger dans l’ordre croissant les fractions suivantes :
13/5 ; 10/5 ; 4/5 ; 6/5 ; 28/5

Ranger dans l’ordre décroissant les fractions suivantes :
7/15 ; 7/3 ; 7/8 ; 7/16 ; 7/31

Exercice N°3

Comparer :
13/27 et 4/9
7/5 et 23/15
3/4 et 73/100
171/130 et 16/13

Exercice N°4

Ranger les fractions suivantes dans l’ordre croissant :

1/3 ; 5/6 ; 11/18 ; 7/9 ; 3/2

Voir les fiches