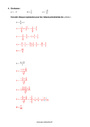Division de fractions - Séquence complète : 2eme Secondaire

Séquence complète sur “Division de fractions” pour la 2eme Secondaire

Notions sur “Les fractions (2)”

Cours sur “Division de fractions” pour la 2eme Secondaire

Propriété :
Diviser par un nombre relatif différent de 0 revient à multiplier par son inverse.
Soient 4 nombres a,b,c et d tels que : b ≠0,c≠0 et d≠0
a/b÷c/d=a/b×d/c=(a×d)/(b×c)

Exemples :
(-2)/7 ÷ 4/5= (-2)/7 × 5/4= (-2×5)/(7×4)= (-2×5)/(7×2×2)= (-5)/14
-3 ÷ 1/4= -3 × 4/1= (-12)/1= -12
(2/5)/((-10)/3)=2/5×(-3)/10=(2×-3)/(5×10)= (2×-3)/(5×2×5)=(-3)/25

Remarque : La barre de fraction principale doit être plus grande et à hauteur du signe =.
Exemples :
A= (3/11)/5= (3/11)/(5/1)=3/11×1/5=3/55
B= 3/(11/5)= (3/1)/(11/5)=3/1×5/11=15/11
C= (5/3-9/4)/(27/10×15/9)=(20/12-27/12)/((27×15)/(10×9))=((20-27)/12)/((9×3×5×3)/(5×2×9))=((-7)/12)/(9/2)=(-7)/12×2/9=(-7×2)/(2×6×9)=(-7)/54

Exercices, révisions sur “Division de fractions” à imprimer avec correction pour la 2eme Secondaire

Consignes pour ces révisions, exercices :

1-Calculer et donner le résultat sous forme d’une fraction simplifiée :

5/6÷6/5= 4/7÷(-2)/7= 11÷22/3=
-2/3÷(-5)/6= (-3)/8÷(-6)/24= (-14)/25÷7/15=
7/11÷(-21)/55= -45/20÷36/(-10)= (-3)/4÷(-5)/28=

2-Calculer et donner le résultat sous forme d’une fraction simplifiée :

A=(1/8-7/12)÷(7/6+7/16)
B=- 1/8-7/12÷7/6+7/12
C=(1/8+7/12)×(6/5÷(-4)/15)

3-Calculer et donner le résultat sous forme d’une fraction simplifiée :

A=(3/8+1/4)÷(4/3-1/6)
B=(1/2+2/3)/(3/4-1/12+1/3)
C=((1/5-2/5×1/3)×(1/12-5/6))/(7/10+1/15)

On donne :
a= -2 b=1/( 4 ) c= (-5)/2

Evaluation, bilan, contrôle avec la correction sur “Division de fractions” pour la 2eme Secondaire

Notions sur la “Les fractions (2)”

Compétences évaluées
Savoir diviser deux fractions
Savoir enchaîner les opérations
Savoir travailler sur un programme utilisant la division de fractions

Consignes pour ces évaluation, bilan, contrôle :

Exercice N°1
Parmi les expressions ci-dessous, indiquer celle qui est égale à :
(-3)/7÷2/(-5)
A= 3/7×2/5 B= 7/(-3)×2/(-5) C= 3/7×5/2

Exercice N°2
Calculer puis donner le résultat sous forme d’une fraction simplifiée :
A= 4/7 ÷(-12)/35 B= (-5)/8 ÷8/5

C= -2 ÷4/9 D= 13/15 ÷39/45

Exercice N°3
Calculer puis donner le résultat sous forme d’une fraction simplifiée :
A= 15/4+5/12÷10/9

B= 6/5+21/5÷14/15

C=(4/5+7/10)÷(5/6-5/8)

Exercice N°4
On donne :
A=(1/6+1/4)÷(-5)/4

B=(1/12÷5/4)+4/(15 )

Montrer que A et B sont deux fractions opposées l’une de l’autre.

Exercice N°5
On donne :
a= (-2)/3

Calculer A et donner le résultat sous forme d’une fraction simplifiée pour :