Nombres et calculs : 3eme Secondaire - PDF à imprimer

Vidéo pédagogique interactive avec La Fée des Maths sur “Ecriture simplifiée des nombres relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Ecriture simplifiée des nombres relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Ecriture simplifiée des nombres relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique…

Vidéo pédagogique interactive avec La Fée des Maths sur “Equation produit nul” pour la 3eme Secondaire . Cette capsule pédagogique sur “Equation produit nul” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Equation produit nul” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices Vidéo de cours…

Vidéo pédagogique interactive avec La Fée des Maths sur “Factoriser à l’aide d’une identité remarquable” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Factoriser à l’aide d’une identité remarquable” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Factoriser à l’aide d’une identité remarquable” permet à l’élève de vérifier qu’il a bien compris la ou les notions…

Vidéo pédagogique interactive avec La Fée des Maths sur “Résoudre une équation” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Résoudre une équation” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Résoudre une équation” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices Vidéo de cours…

Vidéo pédagogique interactive avec La Fée des Maths sur “Carré et racine carrée d’un nombre” pour la 2eme, 3eme Secondaire et : 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Carré et racine carrée d’un nombre” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Carré et racine carrée d’un nombre” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices Vidéo de…

Vidéo pédagogique interactive avec La Fée des Maths sur “Développer avec la double distributivité” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Développer avec la double distributivité” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Développer avec la double distributivité” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique…

Vidéo pédagogique interactive avec La Fée des Maths sur “Les nombres relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Les nombres relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Les nombres relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices Vidéo de cours…

Vidéo pédagogique interactive avec La Fée des Maths sur “Développer et factoriser une expression littérale” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Développer et factoriser une expression littérale” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Développer et factoriser une expression littérale” permet à l’élève de vérifier qu’il a bien compris la ou les notions…

Vidéo pédagogique interactive avec La Fée des Maths sur “Produire et utiliser une expression littérale” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Produire et utiliser une expression littérale” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Produire et utiliser une expression littérale” permet à l’élève de vérifier qu’il a bien compris la ou les notions…

Vidéo pédagogique interactive avec La Fée des Maths sur “Simplifier et réduire une expression littérale” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Simplifier et réduire une expression littérale” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Simplifier et réduire une expression littérale” permet à l’élève de vérifier qu’il a bien compris la ou les notions…

Vidéo pédagogique interactive avec La Fée des Maths sur “Simplifier une fraction” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Simplifier une fraction” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Simplifier une fraction” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices Vidéo de cours…

Vidéo pédagogique interactive avec La Fée des Maths sur “Comparer des nombres relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Comparer des nombres relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Comparer des nombres relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices…

Soustraire des nombres relatifs : 1ere, 2eme, 3eme Secondaire – Vidéo pédagogique – La Fée des Maths…

Suppression de parenthèses : 1ere, 2eme, 3eme Secondaire – Vidéo pédagogique – La Fée des Maths…

Vidéo pédagogique interactive avec La Fée des Maths sur “Tester une égalité” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Tester une égalité” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Tester une égalité” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices  Vidéo de…

Vidéo pédagogique interactive avec La Fée des Maths sur “Priorités opératoires des relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Priorités opératoires des relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Priorités opératoires des relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices…

Vidéo pédagogique interactive avec La Fée des Maths sur “Multiplier des nombres relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Multiplier des nombres relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Multiplier des nombres relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices…

Vidéo pédagogique interactive avec La Fée des Maths sur “Diviser des nombres relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Diviser des nombres relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Diviser des nombres relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices…

Vidéo pédagogique interactive avec La Fée des Maths sur “Développer à l’aide d’une identité remarquable” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Développer à l’aide d’une identité remarquable” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Développer à l’aide d’une identité remarquable” permet à l’élève de vérifier qu’il a bien compris la ou les notions…

Vidéo pédagogique interactive avec La Fée des Maths sur “Additionner des nombres relatifs” pour la 1ere, 2eme, 3eme Secondaire , : 1ere, 2eme, 3eme Secondaire et : 1ere, 2eme, 3eme Secondaire . Cette capsule pédagogique sur “Additionner des nombres relatifs” est une courte vidéo de 3 à 5 minutes ludique avec des exercices interactifs. Cette capsule sur “Additionner des nombres relatifs” permet à l’élève de vérifier qu’il a bien compris la ou les notions abordées. Vidéo pédagogique interactive avec exercices…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Développer à l’aide d’une identité remarquabla 3eme Secondaire Développer une identité remarquable. Développer une expression littérale. Utiliser l’identité remarquable pour du calcul astucieux. Questions de brevet. Pour aller plus loin. Prérequis : cours « Développer et réduire une expression littérale ». Développer avec la simple distributivité : k×(a+b)=k×a + k×b et k×(a-b)=k×a – k×b Développer avec la double distributivité : (a+b)×(c+d)=a×c+a×d+b×c+b×d Supprimer des parenthèses précédées d’un « – » : on change…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Factoriser à l’aide d’une identité remarquabla 3eme Secondaire Factoriser avec une identité remarquable. Factoriser une expression littérale. Questions de brevet. Pour aller plus loin. Prérequis : cours « Factoriser une expression littérale » et « Développer et réduire une expression littérale ». ▸ Factoriser une expression littérale, c’est transformer une somme (ou différence) en un produit. C’est le contraire de développer : → Il faut repérer le facteur commun. → On…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Développer et réduire une expression littérala 3eme Secondaire Simplifier une expression littérale sans parenthèses. Développer une expression littérale avec des parenthèses avec la distributivité. Questions de brevet. Pour aller plus loin. Prérequis : Une expression littérale est une suite d’un ou plusieurs calculs contenant au moins une lettre. Règles d’écriture: On peut supprimer le signe lorsqu’il est suivi d’une lettre ou d’une parenthèse : Cas particulier :…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Décomposer un nombre en produit de facteurs premiers : 3eme Secondaire Les nombres premiers : introduction. Décomposer un nombre en un produit de facteurs premiers. Simplifier des fractions avec la décomposition en produit de facteurs premiers. Questions de brevet. Pour aller plus loin. Les nombres premiers : introduction. Déterminer si un nombre est premier ou non. Il n’existe pas de façon simple au collège de déterminer si…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Résoudre une équation produit nul ou racine carrée : 3eme Secondaire Résoudre une équation produit nul. Résoudre une équation racine carrée. Ramener une équation à une équation de type produit nul ou racine carrée. Questions de brevet. Pour aller plus loin. Résoudre une équation produit nul. Méthode pour résoudre une équation produit nul Etape ① : j’identifie le type d’équation, et si besoin, je factorise afin de…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Résoudre une équation du premier degré : 3eme Secondaire Vérifier qu’un nombre est solution d’une équation. Résoudre une équation. Poser une équation. Questions de brevet. Pour aller plus loin. Vérifier qu’un nombre est solution d’une équation. Méthode pour vérifier qu’un nombre est solution d’une équation. Etape ① : je remplace l’inconnue (le plus souvent x) par la valeur donnée dans le membre de gauche de l’équation et…

Je révise mon : 3eme Secondaire pas à pas avec Mon Pass Maths. Puissances d’exposants positifs ou négatifs : 3eme Secondaire Écrire sous forme de puissance. Écrire une puissance sous forme décimale. Calculer en respectant les priorités opératoires. Résoudre les problèmes utilisant les puissances d’exposants positifs ou négatifs. Questions de brevet. Pour aller plus loin. Écrire sous forme de puissance. Méthode pour écrire sous forme de puissance. Etape ① : je repère le terme répété en multiplication et je compte…

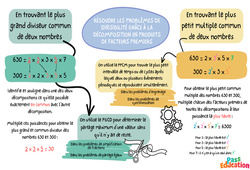
Carte mentale en nombres et calculs pour la 2eme, 3eme Secondaire et : 2eme, 3eme Secondaire sur résoudre les problèmes de divisibilité grâce à la décomposition en produits de facteurs premiers. En trouvant le plus grand diviseur commun de deux nombres Identifie et souligne dans une des deux décompositions ce qu’elle possède exactement en commun avec l’autre décomposition. Multiplie ces puissances pour obtenir le plus grand et commun diviseur des nombres 630 et 300 : 2 x 3 x 5…

Cours, exercices et évaluation avec la correction niveau : 3eme Secondaire sur les critères de divisibilité et résolution de problèmes. Cours niveau : 3eme Secondaire sur les critères de divisibilité et résolution de problèmes.  Division euclidienne Définition (division euclidienne de a par b) : a et b sont des nombres entiers positifs, avec b≠0. Effectuer la division euclidienne de a par b, c’est trouver deux nombres entiers positifs q et r tels que a=b×q+r avec r<b. Rappel : a=b×q+r…

Cours niveau : 3eme Secondaire sur les critères de divisibilité et résolution de problèmes.  Division euclidienne Définition (division euclidienne de a par b) : a et b sont des nombres entiers positifs, avec b≠0. Effectuer la division euclidienne de a par b, c’est trouver deux nombres entiers positifs q et r tels que a=b×q+r avec r<b. Rappel : a=b×q+r  Diviseurs et multiples d’un nombre Définition : Si r=0, on obtient a=b×q. On dit que b est un diviseur…